Hydrogen Fuel Cell
Hydrogen and oxygen can be combined in a fuel cell to produce electrical energy. A fuel cell uses a chemical reaction to provide an external voltage, as does a battery, but differs from a battery in that the fuel is continually supplied in the form of hydrogen and oxygen gas. It can produce electrical energy at a higher efficiency than just burning the hydrogen to produce heat to drive a generator because it is not subject to the thermal bottleneck from the second law of thermodynamics. It's only product is water, so it is pollution-free. All these features have led to periodic great excitement about its potential, but we are still in the process of developing that potential as a pollution-free, efficient energy source (see Kartha and Grimes).
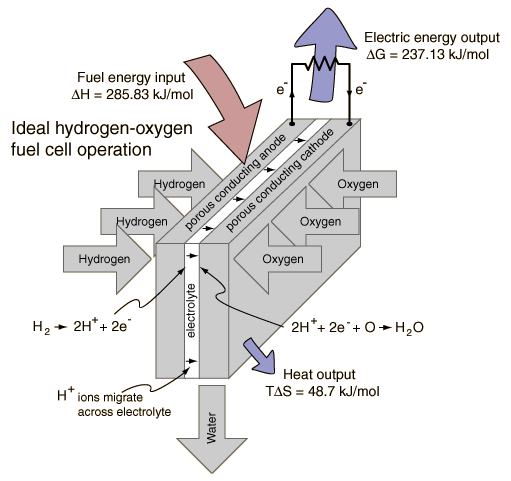
Combining a mole of hydrogen gas and a half-mole of oxygen gas from their normal diatomic forms produces a mole of water. A detailed analysis of the process makes use of the thermodynamic potentials. This process is presumed to be at 298K and one atmosphere pressure, and the relevant values are taken from a table of thermodynamic properties.
| Quantity | H2 | 0.5 O2 | H2O | Change |
| Enthalpy | 0 | 0 | -285.83 kJ | DH = -285.83 kJ |
| Entropy | 130.68 J/K | 0.5 x 205.14 J/K | 69.91 J/K | TDS = -48.7 kJ |
Energy is provided by the combining of the atoms and from the decrease of the volume of the gases. Both of those are included in the change in enthalpy included in the table above. At temperature 298K and one atmosphere pressure, the system work is
Since the enthalpy H= U+PV, the change in internal energy U is then
The entropy of the gases decreases by 48.7 kJ in the process of combination since the number of water molecules is less than the number of hydrogen and oxygen molecules combining. Since the total entropy will not decrease in the reaction, the excess entropy in the amount TDS must be expelled to the environment as heat at temperature T. The amount of energy per mole of hydrogen which can be provided as electrical energy is the change in the Gibbs free energy:
For this ideal case, the fuel energy is converted to electrical energy at an efficiency of 237.1/285.8 x100% = 83%! This is far greater than the ideal efficiency of a generating facility which burned the hydrogen and used the heat to power a generator! Although real fuel cells do not approach that ideal efficiency, they are still much more efficient than any electric power plant which burns a fuel.
In comparing the fuel cell process to its reverse reaction, electrolysis of water, it is useful treat the enthalpy change as the overall energy change. The Gibbs free energy is that which you actually have to supply if you want to drive a reaction, or the amount that you can actually get out if the reaction is working for you. So in the electrolysis/fuel cell pair where the enthalpy change is 285.8 kJ, you have to put in 237 kJ of energy to drive electrolysis and the heat from the environment will contribute TDS=48.7 kJ to help you. Going the other way in the fuel cell, you can get out the 237 kJ as electric energy, but have to dump TDS = 48.7 kJ to the environment.